Цифры числа \(e\)#

Число \(e\) на калькуляторе#

Когда я учился в школе, моей любимый игрушкой был инженерный калькулятор. Его табло вмещало \(10\) цифр, и число \(e\) на нём выглядело вот так:

euler_number

Любопытный факт

По забавному совпадению цифр число \(e\) имеет прозвище «два и семь, два Толстых», ведь 1828 — год рождения Льва Толстого.

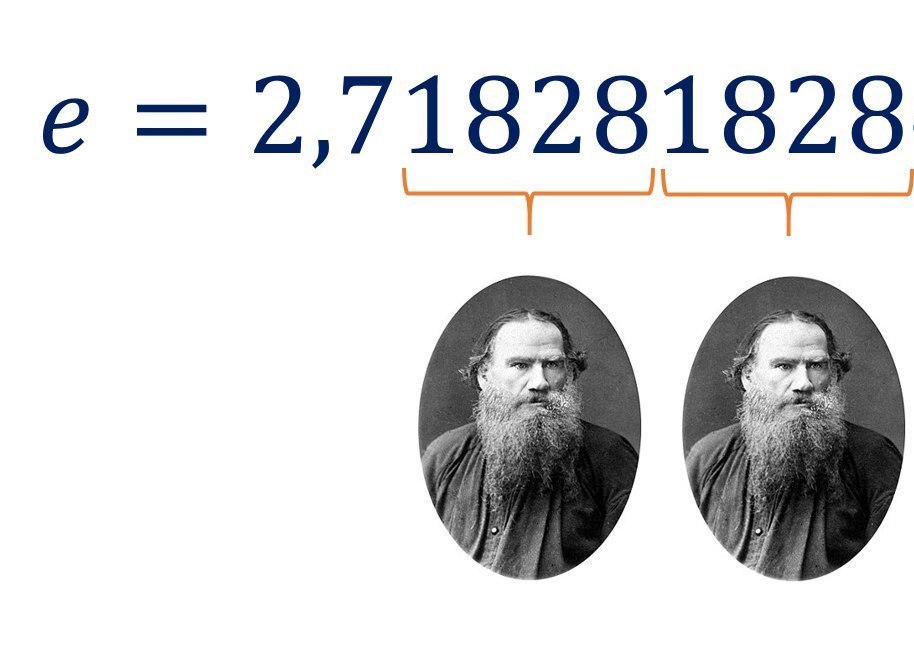
2*tolstoy

Намёк на рациональность#

Там, где два Толстых, вполне могло бы случиться и три, и четыре, и вообще бесконечное их количество. В последнем случае число \(e\) оказалось бы периодической десятичной дробью

(1)#\[e \stackrel{?}{=} 2.7182818281828\ldots \equiv 2.7(1828)\]

Если равенство (1) верно, то число \(e\) должно быть рациональным. Это прямое следствие следующей теоремы:

Theorem

Всякая периодическая десятичная дробь является рациональным числом, то есть может быть записана в виде отношения двух целых чисел.

Вот несколько примеров превращения периодической десятичной дроби в обыкновенную:

  • \(0.166666\ldots \equiv 0.1(6) = \frac 16\)

  • \(2.363636\ldots \equiv 2.(36) = \frac {26}{11}\)

  • \(-1.25 \equiv -1.25(0) = -\frac 54\)

  • \(3.142857142857\ldots \equiv 3.(142857) = 3 + \frac 17 = \frac{22}7\)

Как происходят такие превращения?

Возьмём для примера периодическую дробь \(x = 2.(36)\). Выделим целую часть:

\[ x = 2 + y,\quad y = 0.(36). \]

Чтобы найти \(y\), домножим его на \(100 = 10^2\) (десять в степени длина периода). Получаем

\[ 100 y = 36.(36) = 36 + 0.(36) = 36 + y. \]

Из этого уравнения находим, что

\[ y = \frac{36}{100 - 1} = \frac{36}{99} = \frac{4}{11}, \]

и поэтому \(x = 2 + y = 2\frac 4{11} = \frac{26}{11}\).

Hint

Записав \(2.7(18) = 2.7 + 0.1x\), выразите \(100x\) через \(x\).

Число \(e\) на компьютере#

Так совпало, что на калькуляторе с десятью разрядами число \(e\) смахивает на периодическую десятичную дробь (1). Однако если вооружиться калькулятором побольше или компьютером, то таких иллюзий не возникнет. Вот как выглядят \(16\) первых цифр числа \(e\):

import math 
print(math.e)

2.718281828459045

Дополнительные к двум Толстым 6 цифр образуют углы равнобедренного прямоугольного треугольника, что позволяет немного расширить мнемоническое правило для запоминания цифр числа \(e\):

euler_mnemonic

Warning

Разумеется, даже этими цифрами число \(e\) не исчерпывается. Скоро мы докажем, что число \(e\) иррационально, а это означает, что

  • \(е \ne \frac mn\) ни при каких целых числах \(m\) и \(n\);

  • \(e = \overline{a_0.a_1a_2\ldots a_n \ldots}\) — бесконечная непериодическая десятичная дробь.

Компьютеры используют стандартный тип double для записи десятичных дробей, который обычно позволяет хранить только \(16\) цифр после десятичной точки. Если же использовать библиотеку decimal языка Python, то можно раздобыть сколько душе угодно1 верных десятичных знаков числа \(e\). Например, \(100\):

from decimal import Decimal, getcontext
getcontext().prec=100
print(Decimal.exp(Decimal(1)))

2.718281828459045235360287471352662497757247093699959574966967627724076630353547594571382178525166427
https://blog.reface.ai/content/images/2021/04/0_Mi-xBLF3U-58Eu76.png

Вычисление верных десятичных знаков знаменитых иррациональных чисел, таких как \(\pi\), \(e\), \(\sqrt 2\), \(\varphi = \frac {\sqrt 5 - 1}2\) (золотое сечение), представляет собой своеобразный вид спорта. Первоначальные вехи на этом пути в отношении числа \(e\) перечислены в следующей таблице из википедии:

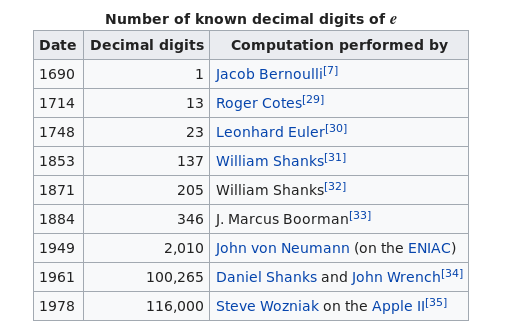
euler_decimals

Далее резко возросшая вычислительная мощность компьютеров позволила вычислять миллионы, миллиарды и даже триллионы цифр числа \(e\). На конец 2020 года рекорд составляет свыше \(31\) триллиона десятичных знаков.

Десятичные приближения числа \(e\)#

Чем больше цифр взять, тем точнее получится приближение к истинному значению числа \(e\): обрубая бесконечную десятичную дробь

\[ e = \overline{2.71828\ldots a_{n-1} a_n \ldots}, \]

после \(a_{n-1}\), получаем конечную десятичную дробь

\[ e_n = \overline{2.71828\ldots a_{n-1}}, \quad e \approx e_n. \]

Погрешность такого приближения равна

\[ r_n = e - e_n = \overline{\underbrace{0.00\ldots 0}_{n\text{ нулей}} a_n \ldots} = \frac{a_n}{10^n} + \frac{a_{n+1}}{10^{n+1}} + \ldots \]

Это заведомо меньше, чем

\[ \underbrace{0.00\ldots 0}_{n\text{ нулей}} (9) = \underbrace{0.00\ldots 0}_{n - 1\text{ нуль}}1 = \frac 1{10^{n-1}}. \]

Вывод

Если взять приближение числа \(e\), содержащее \(n\) его верных десятичных знаков (включая целую часть), то погрешность приближения \(r_n\) удовлетворяет неравенству \(0 \leqslant r_n \leqslant \frac 1{10^{n-1}}\).

Задачи#

  1. Запишите число (1) в виде несократимой дроби \(\frac mn\).

  2. Назовём число счастливым, если в десятичной записи оно имеет одинаковые четвёрки цифр на позициях со 2-й по 5-ю и с 6-й по 9-ю после десятичной точки:

    \[ \ldots\bullet.\bullet abcdabcd\bullet\ldots \]

    Например, число \(e\) счастливое. Какова вероятность того, что наугад взятое число счастливое?

  3. Рекорд 2020 года содержит \(31\,415\,926\,535\,897\) верных десятичных знаков числа \(e\). Что за странное число? Почему именно столько?

  4. Докажите равенство \(\underbrace{0.00\ldots 0}_{n\text{ нулей}} (9) = \underbrace{0.00\ldots 0}_{n - 1\text{ нуль}}1.\)

  5. 💻 Число \(\alpha \in \mathbb R\) называется нормальным, если в его десятичной записи все \(10\) цифр встречаются в равной пропорции, т.е. доля каждой составляет \(10\%\) (в математике это называется равномерное распределение). Подсчитайте, сколько раз встречается каждая цифра в первых \(100\), \(1000\), \(10000\) десятичных знаках числа \(e\). Похоже ли, что число \(e\) нормальное?

1

Лишь бы хватило оперативы