Число \(e\) в математике#

В предыдущих главах мы получили несколько представлений числа \(e\):

  • определение (2): \(e = \lim\limits_{n\to\infty} \big(1 + \frac 1n\big)^n\);

  • сумма ряда (4): \(e = \sum\limits_{n=0}^\infty \frac 1{n!}\);

  • цепная дробь (9): \(e = [2; 1, 2, 1, 1, 4, 1, 1, 6, 1, \ldots]\).

Сюда же можно отнести привычную нам запись десятичной дробью:

(13)#\[ e = a_0 + \frac{a_1}{10} + \frac{a_2}{100} + \ldots + \frac{a_n}{10^n} + \ldots, \quad a_k \in \{0, \ldots, 9\},\]

где цифры \(a_0 = 2\), \(a_1 = 7\), \(a_2 = 1\) и т.д. Внимательный читатель заметит, что (13) тоже представляет собой сумму ряда, только в отличие (4) у его членов нет явной закономерности: каждая следующая цифра \(a_k\) может быть любой. Все четыре подхода роднит между собой одно обстоятельство: в каждом случае число \(e\) получается как предел некоторой последовательности рациональных чисел.

В принципе любое иррациональное число определяется сходным образом. Однако число \(e\) настолько особенное, что для него было найдено множество эквивалентных представлений. Все они так или иначе связаны с предельным переходом.

Число \(e\) встречается ещё много где в математике.

Площадь под графиком гиперболы#

Число \(e\) можно определить геометрически. Рассмотрим криволинейную трапецию под графиком гиперболы \(y=\frac 1x\). Зафиксируем левую границу трапеции в точке \(a=1\). Меняя правую границу \(b > 1\), можно увеличивать или уменьшать площадь \(S\) синей трапеции.

../_images/00261ca4b2cf0517011f895a5d74d05e20ce6829ef4878d50fe67e4941e5f6a6.svg
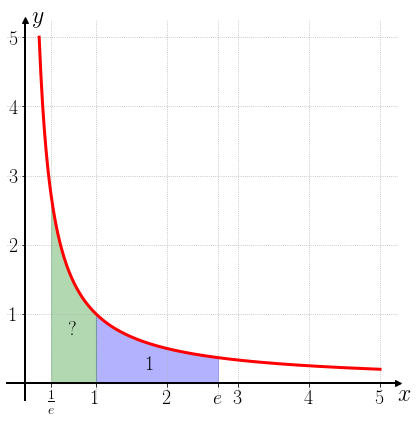
../_images/hyp1.png

Существует ровно одно число \(b\), при котором эта площадь равна единице. Это и есть число \(e\).

Hint

../_images/hyperbolae.svg

Вероятностная интерпретация#

Пример из википедии

Будем складывать случайные числа из отрезка \([0;1]\) до тех пор, пока их сумма не превысит \(1\). Чему равно математическое ожидание числа слагаемых?

Приблизительно решить подобную задачу можно очень легко с помощью компьютера. Будем складывать случайные числа, пока их сумма не превзойдёт \(1\). Повторив этот эксперимент \(N\) раз, вычислим среднее значение числа слагаемых в каждом опыте. Это и будет приближением искомого математического ожидания.

Этот план реализует следующая функция estimate_average(N).

from random import random 

def estimate_average(N):
    total_summands = 0
    for _ in range(N):
        s = 0
        while s <= 1:
            s += random()
            total_summands += 1
    return total_summands / N

Теперь запустим эту функцию для \(N= 10, 100, 1000, 10^4, 10^5, 10^6, 10^7\).

for n in [10**i for i in range(1, 8)]:
    print(f"N={n}, average number of summands = {estimate_average(n)}")

N=10, average number of summands = 2.9
N=100, average number of summands = 2.55
N=1000, average number of summands = 2.716
N=10000, average number of summands = 2.7206
N=100000, average number of summands = 2.71758

N=1000000, average number of summands = 2.717244

N=10000000, average number of summands = 2.7181063

Видно, что чем больше \(N\), тем ближе результат к числу \(e\). Впрочем, сходимость тут довольно медленная, что в целом характерно для такого рода вероятностных алгоритмов.

Warning

Разумеется, приведённые расчёты ни в коей мере не являются доказательством того, что искомое среднее значение равно \(e\). Они лишь наводят на мысль о справедливости этой гипотезы. Знакомые с теорией вероятностей читатели могут попробовать доказать сию гипотезу строго математически (см. ниже задачу 2).

Эффективность систем счисления#

Посмотрим внимательнее на ответы в двух последних задачах.

  • в первом случае мы получили \(10^2 = 10^{\frac{20}{10}}= q^{\frac nq}\), где \(n=20\) — число цифр, \(q=10\) — основание десятичной системы счисления;

  • во втором случае ответ был \(2^{10} = 2^{\frac{20}{2}}= q^{\frac nq}\), где \(n=20\) — число цифр, \(q=2\) — основание двоичной системы счисления.

В общем случае, если у вас есть \(n\) цифр в \(q\)-ичной системе счисления, то в лучшем случае вы можете составить из них \(q^{\frac nq}\) различных чисел. Чем больше это значение, тем больше различных чисел можно закодировать набором цифр фиксированной длины, и тем более эффективна система счисления. Оценить эффективность системы счисления в зависимости от её основания \(q\) можно на следующем графике:

../_images/3df7d2bcfbffd9c3acded8a199cfa58796333a7c941226ebaeec37005d2a8d5c.svg

Оказывается, что самая эффективная система счисления имеет основание \(q=e\), а самое выгодное натуральное основание — тройка. И чем больше \(n\) (количество цифр), тем заметнее преимущество этих оснований над привычной нам десятичной системой счисления.

Факториал#

Вернёмся к нашему старому знакомцу — факториалу: \(n! = 1 \cdot 2 \cdot \ldots \cdot n\).

Комбинаторный смысл факториала

Количество различных перестановок \(n\) объектов равно \(n!\).

И это количество растёт очень быстро: уже \(10!\) превосходит миллион, а \(15!\) — триллион. Такая стремительная скорость роста факториала в значительной степени объясняет крайне быструю скорость сходимости ряда (4) к числу \(e\).

Факториал также тесно связан с числом \(e\) великой и могучей формулой Стирлинга:

\[ n! \approx \Big(\frac ne\Big)^n \sqrt{2\pi n}. \]

Посмотрим, насколько хорошо факториал приближается формулой Стирлинга при небольших \(n\). Приближение Стирлинга обозначим через \(d_n\).

Hide code cell source 
import math

factorial = 1
for n in range(1, 11):
    d_n = (n / math.e) ** n * math.sqrt(2 * math.pi * n)
    print(f"n = {n}, n! = {factorial}, d_n = {d_n}")
    print(f"   |n! - d_n| = {abs(factorial - d_n):.6f}, |n! - d_n|/n! = {abs(factorial - d_n) / factorial:.6f}")
    factorial *= n + 1

n = 1, n! = 1, d_n = 0.9221370088957891
   |n! - d_n| = 0.077863, |n! - d_n|/n! = 0.077863
n = 2, n! = 2, d_n = 1.9190043514889832
   |n! - d_n| = 0.080996, |n! - d_n|/n! = 0.040498
n = 3, n! = 6, d_n = 5.836209591345864
   |n! - d_n| = 0.163790, |n! - d_n|/n! = 0.027298
n = 4, n! = 24, d_n = 23.506175132893294
   |n! - d_n| = 0.493825, |n! - d_n|/n! = 0.020576
n = 5, n! = 120, d_n = 118.0191679575901
   |n! - d_n| = 1.980832, |n! - d_n|/n! = 0.016507
n = 6, n! = 720, d_n = 710.078184642185
   |n! - d_n| = 9.921815, |n! - d_n|/n! = 0.013780
n = 7, n! = 5040, d_n = 4980.395831612462
   |n! - d_n| = 59.604168, |n! - d_n|/n! = 0.011826
n = 8, n! = 40320, d_n = 39902.39545265671
   |n! - d_n| = 417.604547, |n! - d_n|/n! = 0.010357
n = 9, n! = 362880, d_n = 359536.87284194835
   |n! - d_n| = 3343.127158, |n! - d_n|/n! = 0.009213
n = 10, n! = 3628800, d_n = 3598695.6187410373
   |n! - d_n| = 30104.381259, |n! - d_n|/n! = 0.008296

Видно, что абсолютная погрешность \(\vert n! - d_n \vert\) быстро растёт, а вот относительная погрешность \(\frac{\vert n! - d_n \vert}{n!}\) уменьшается с ростом \(n\). Более наглядно это можно проследить в следующей таблице:

Table 3 Погрешность оценки факториала формулой Стирлинга#

\(n\)

\(n!\)

\(d_n\)

\(\vert n! - d_n\vert\)

\(\frac{\vert n! - d_n\vert}{n!}\)

1

1

0.922137

0.077863

0.077863

2

2

1.919004

0.080996

0.040498

3

6

5.836210

0.163790

0.027298

4

24

23.506175

0.493825

0.020576

5

120

118.019168

1.980832

0.016507

6

720

710.078185

9.921815

0.013780

7

5040

4980.395832

59.604168

0.011826

8

40320

39902.395453

417.604547

0.010357

9

362880

359536.872842

3343.127158

0.009213

10

3628800

3.598696e+06

3.010438e+04

0.008296

11

39916800

3.961563e+07

3.011749e+05

0.007545

12

479001600

4.756875e+08

3.314114e+06

0.006919

13

6227020800

6.187239e+09

3.978132e+07

0.006389

14

87178291200

8.666100e+10

5.172895e+08

0.005934

15

1307674368000

1.300431e+12

7.243646e+09

0.005539

Подробнее о различных вариантах формулы Стирлинга, а также о рядах Стирлинга можно прочитать в статье Оценки факториала и формула Стирлинга (c. 71—77).

Беспорядки и субфакториалы#

Определение

Перестановка \(n\) объектов называется беспорядком, если она не содержит неподвижных элементов. Иначе говоря, никто из \(n\) джентльменов не взял свою шляпу.

Общее количество \(n\)-беспорядков обозначается \(!n\) (читается субфакториал-эн). Например:

  • \(!1 = 0\), так как в единственной перестановке из одного элемента он находится на своём месте;

  • \(!2 = 1\), ведь из двух перестановок \(12\) и \(21\) беспорядком является только вторая;

  • \(!3 = 2\), как мы видели в задаче о джентльменах и их шляпах.

По определению полагают \(!0 = 1\).

Вычислять субфакториал, перебирая все возможные перестановки, довольно утомительно уже при \(n=4\). Нет ли способа попроще? Конечно же, есть! Оказывается, что для субфакториала справедлива такая же рекуррентная формула, как и для факториала:

\[ !(n+1) = n\cdot(!n + !(n-1)). \]

Отсюда получаем, например, что

\[ !4 = 3\cdot(!3 + !2) = 3 \cdot(2 + 1) = 9, \]
\[ !5 = 4\cdot(!4 + !3) = 4 \cdot(9+2) = 44. \]

Примерно таким образом компьютеры и вычисляют субфакториалы. Ниже приведёт код, который одновременно выводи факториал и субфакториал \(n\) для \(0\leqslant n < 10\).

from scipy.special import factorial
from sympy import subfactorial

for n in range(10):
    print(f"n = {n}, n! = {factorial(n, exact=True)}, !n = {subfactorial(n)}")

n = 0, n! = 1, !n = 1
n = 1, n! = 1, !n = 0
n = 2, n! = 2, !n = 1
n = 3, n! = 6, !n = 2
n = 4, n! = 24, !n = 9
n = 5, n! = 120, !n = 44
n = 6, n! = 720, !n = 265
n = 7, n! = 5040, !n = 1854
n = 8, n! = 40320, !n = 14833
n = 9, n! = 362880, !n = 133496

Вы спросите, где же тут число \(e\)? А попробуйте вдобавок вывести отношение \(\frac{n!}{!n}\) при \(n>1\). Получится примерно следующее:

Table 4 Факториалы и субфакториалы#

\(n\)

\(n!\)

\(!n\)

\(\frac{n!}{!n}\)

True digits

\(4\)

\(24\)

\(9\)

\(\mathbf{2}.(6)\)

\(1\)

\(5\)

\(120\)

\(44\)

\(\mathbf{2.7}2(72)\)

\(2\)

\(6\)

\(720\)

\(265\)

\(\mathbf{2.71}698\ldots\)

\(3\)

\(7\)

\(5040\)

\(1854\)

\(\mathbf{2.718}4466\dots\)

\(4\)

\(8\)

\(40320\)

\(14833\)

\(\mathbf{2.7182}63331\ldots\)

\(5\)

\(9\)

\(362880\)

\(133496\)

\(\mathbf{2.71828}369\ldots\)

\(6\)

\(10\)

\(3628800\)

\(1334961\)

\(\mathbf{2.718281}657\ldots\)

\(7\)

Явно прослеживается закономерность

(14)#\[ \lim\limits_{n\to\infty}\frac{n!}{!n} = e.\]

Переворачивая дробь, можно переписать этот предел как

\[ \lim\limits_{n\to\infty}\frac{!n}{n!} = \frac 1e. \]

Таким образом, доля беспорядков составляет примерно \(\frac 1e\) от числа всех перестановок.

Из таблицы 4 также можно заметить, что сходимость в (14) почти такая же быстрая, как и для частичных сумм ряда (4). Что бы и видим на следующем графике:

../_images/0173138f59ec38449f8b71ca0be29760f3cb8b3bc15dce8f80a1d73603afce64.svg

Задачи#

  1. Пусть \(S(b)\) — площадь криволинейной трапеции под графиком гиперболы \(y = \frac 1x\), построенной по отрезку \([1; b]\), \(b > 1\). Определим \(S(a) = - S\big(\frac 1a \big)\) при \(0 < a < 1\). Докажите, что \(S(bc) = S(b) + S(c)\) при всех \(b, c > 0\).

  2. Пусть \(\xi_1, \xi_2, \ldots, \xi_n, \ldots\) — независимые случайные величины, равномерно распределённые на отрезке \([0; 1]\) и

    \[ \eta = \min\{n\colon \xi_1 + \ldots + \xi_n > 1\}. \]

    Докажите, что \(\mathbb E\eta = e\).

  3. Докажите, что функция \(f(x) = x^{\frac n x}\) имеет глобальный максимум в точке \(x = e\) при любом \(n\in \mathbb N\).

  4. 💻 Вычислите абсолютную и относительную погрешность приближения факториала уточнённой формулой Стирлинга

    \[ n! \approx \Big(\frac ne\Big)^n \sqrt{2\pi n} \Big(1 + \frac 1{12n}\Big). \]

    Сравните полученные результаты с данными из таблицы таблицы 3.

  5. Докажите равенство

    \[ !n = n!\left(1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+ \ldots +(-1)^n\frac{1}{n!}\right). \]

    Указание. Вам может пригодиться формула включений-исключений.

  6. Докажите равенство \(!(n+1) = n\cdot(!n + !(n-1))\).