Эйлер вступает в дело#
Принцип Арнольда
Если какое-либо понятие имеет персональное имя, то это – не имя первооткрывателя.

Fig. 2 В. И. Арнольд#

Fig. 3 Леонард Эйлер#
Вот и число \(e\) открыл Яков Бернулли, а названо оно в честь другого швейцарского математика Леонарда Эйлера (1707 — 1783), долгое время работавшего в России. Впрочем, это неспроста: Эйлер открыл несколько поистине замечательных представлений числа \(e\).
Число \(e\) в виде ряда#
Например, Эйлер установил, что
Что это за странные восклицательные знаки?
Факториал натурального числа \(n\) равен \(n! = 1 \cdot 2 \cdot \ldots \cdot n.\) Например:
\(1! = 1\);
\(2! = 1 \cdot 2 = 2\);
\(3! = 1 \cdot 2 \cdot 3 = 6\);
\(4! = 1 \cdot 2 \cdot 3 \cdot 4 = 24\).
По определению полагают \(0! = 1\).
А как понимать бесконечную сумму?
Прежде всего введём обозначение для конечной суммы от \(0\) до \(n\):
Бесконечная сумма вида (4) называется рядом, а конечная сумма (5) называется частичной суммой этого ряда. По определению суммой ряда (4) называется предел его частичных сумм:
Замечание о работе с бесконечными суммами
Для корректной работы с рядами крайне важно существование предела его частичных сумм, или, как говорят, сходимость ряда. Оперируя с расходящимися рядами, можно легко получить весьма неожиданные результаты. Например, группируя слагаемые ряда
различными способами, получаем, что его сумма равна двум разным значениям:
А всё потому, что этот ряд расходится, т.е. предел его частичных сумм не существует, и указанные группировки слагаемых проводить некорректно.
Повычисляем частичные суммы (5) при небольших значениях \(n\). Ясно, что \(s_0 = 1\), \(s_1 = 1 + \frac 1{1!} = 1+1 = 2\).
При \(n > 3\) частичную сумму (5) предоставим вычислить компьютеру.
Show code cell source
denominator = 1
partial_sum = 1
for n in range(1, 10):
denominator *= n
partial_sum += 1./denominator
print(f"n = {n}, s_n = {partial_sum}")
n = 1, s_n = 2.0
n = 2, s_n = 2.5
n = 3, s_n = 2.6666666666666665
n = 4, s_n = 2.708333333333333
n = 5, s_n = 2.7166666666666663
n = 6, s_n = 2.7180555555555554
n = 7, s_n = 2.7182539682539684
n = 8, s_n = 2.71827876984127
n = 9, s_n = 2.7182815255731922
Результаты вычислений оформим в виде таблицы, в которой частичная сумма \(s_n\) записана в трёх формах: обыкновенная дробь, смешанное число и десятичная дробь. Последний столбец показывает количество верных десятичных знаков числа \(e\) в зависимости от \(n\).
\(n\) |
\(s_n \text{ (frac)}\) |
\(s_n \text{ (mixed)}\) |
\(s_n \text{ (dec)}\) |
True digits |
|---|---|---|---|---|
\(4\) |
\(\frac{65}{24}\) |
\(2\frac{17}{24}\) |
\(\mathbf{2.7}08(3)\) |
\(2\) |
\(5\) |
\(\frac{163}{60}\) |
\(2\frac{43}{60}\) |
\(\mathbf{2.71}(6)\) |
\(3\) |
\(6\) |
\(\frac{1957}{720}\) |
\(2\frac{517}{720}\) |
\(\mathbf{2.718}0(5)\) |
\(4\) |
\(7\) |
\(\frac{685}{252}\) |
\(2\frac{181}{252}\) |
\(\mathbf{2.7182}53968\dots\) |
\(5\) |
\(8\) |
\(\frac{109601}{40320}\) |
\(2\frac{28961}{40320}\) |
\(\mathbf{2.7182}787698\ldots\) |
\(5\) |
\(9\) |
\(\frac{98641}{36288}\) |
\(2\frac{26065}{36288}\) |
\(\mathbf{2.718281}52557\ldots\) |
\(7\) |
\(10\) |
\(\frac{9864101}{3628800}\) |
\(2\frac{2606501}{3628800}\) |
\(\mathbf{2.7182818}01146\ldots\) |
\(8\) |
Связь с определением#
В предыдущей главе мы определили число \(e\) по формуле (2). Настало время выяснить, как оно увязывается с равенством (4).
Для начала нарисуем графики величин \(s_n\) и \(x_n=\big(1 + \frac 1n\big)^n\) как функций от \(n\).
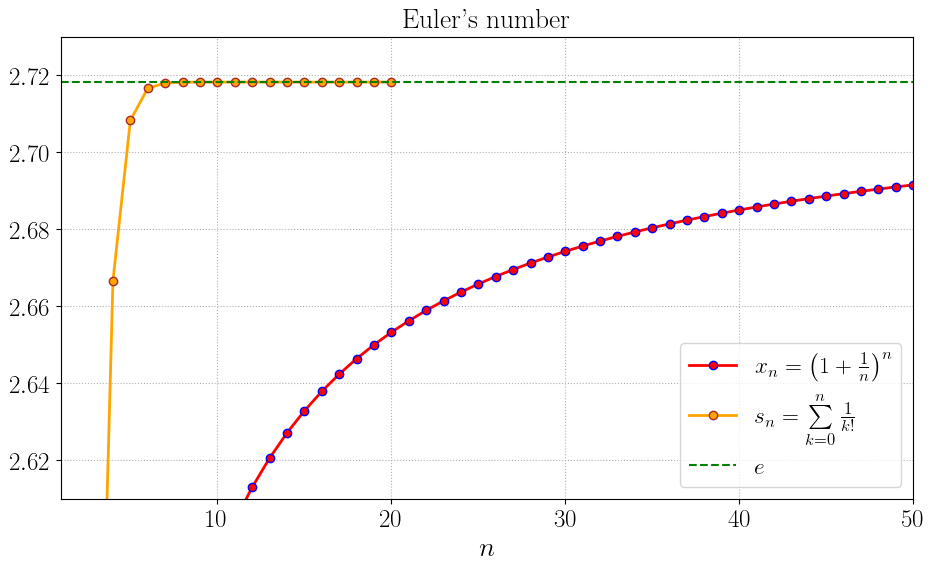
Хорошо видно, что последовательность \(s_n\) очень быстро сходится к числу \(e\): оранжевая линия при \(n > 8\) сливается с пунктирной зелёной линией, соответствующей числу \(e\). Обратите внимание на разительный контраст с поведением красной линии! Последовательность \(x_n = \big(1 + \frac 1n\big)^n\) из определения числа \(e\) сходится к нему гораздо медленнее, чем последовательность частичных сумм (5).
Следующая теорема строго математически устанавливает, что \(\lim\limits_{n\to\infty} s_n =e\).
Theorem
Последовательности \((s_n)\) и \((x_n)\) имеют одинаковый предел, т.е.
Доказательство
Применим бином Ньютона \((1+x)^n = \sum\limits_{k=0}^n \binom nk x^k\) к последовательности \((x_n)\):
Биномиальный коэффициент \(\binom nk\), равный количеству способов выбрать \(k\) объектов из \(n\), можно записать как
где \(n^{\underline k} = n\cdot(n-1)\cdot \ldots \cdot (n-k+1)\) — убывающая факториальная степень. С помощью этого обозначения перепишем формулу (6):
Из неравенства \(n^{\underline k} \leqslant n^k\) следует, что
Устремляя здесь \(n\) к \(\infty\), приходим к неравенству \(e \leqslant \lim\limits_{n\to\infty} s_n\). Чтобы получить неравенство в другую сторону, обрежем сумму в (6), взяв первые \(m\) слагаемых, \(0 < m < n\):
Зафиксируем \(m \in \mathbb N\) и перейдём здесь к пределу при \(n\to \infty\); учитывая, что \(\lim\limits_{n\to\infty} \frac{n^{\underline k}}{n^k} = 1\), получаем
Левая часть по определению равна \(e\), следовательно \(e \geqslant s_m\) при всех \(m \in \mathbb N\). Устремив \(m\to \infty\), находим, что \(e \geqslant \lim\limits_{m\to\infty}s_m\). Вместе с полученным ранее противоположным неравенством это гарантирует, что
Оценка погрешности#
Представление числа \(e\) числовым рядом (4) очень полезно для практических вычислений из-за чрезвычайно быстрой сходимости его частичных сумм \(s_n\) к числу \(e\). Рекорды по вычислению цифр числа \(e\) были установлены именно путём вычисления \(s_n\) при достаточно большом \(n\). Оценить точность приближения помогает следующая оценка погрешности:
Здесь \(\theta_n\) — это просто какое-то число из интервала \((0;1)\). Чему равно \(\theta_n\) при небольших значениях \(n\), можно легко проверить экспериментально.
Show code cell source
import math
denominator = 1
partial_sum = 1
for n in range(1, 10):
denominator *= n
partial_sum += 1./denominator
theta_n = (math.e - partial_sum) * n * denominator
print(f"n = {n}, theta_n = {theta_n}")
n = 1, theta_n = 0.7182818284590451
n = 2, theta_n = 0.8731273138361804
n = 3, theta_n = 0.9290729122628143
n = 4, theta_n = 0.9550555320683571
n = 5, theta_n = 0.9690970754272499
n = 6, theta_n = 0.9774989430752612
n = 7, theta_n = 0.9829080351068242
n = 8, theta_n = 0.9865877495212771
n = 9, theta_n = 0.9892009645173516
Равенство (7) позволяет оценить, сколько верных цифр числа \(e\) даёт приближение \(s_n\) при заданном \(n\). Например, при \(n=5\) имеем
это означает, \(s_5\) даёт как минимум два верных десятичных знака числа \(e\). Это вполне согласуется с данными из таблицы 1.
Иррациональность числа \(e\)#
Оценка погрешности (7) полезна не только для практических вычислений, но и для доказательства теоретических фактов о числе \(e\).
Theorem
Число \(e\) иррационально, т.е. \(e \ne \frac mn\) ни при каких целых числах \(m\) и \(n\).
Proof. Иррациональность обычно доказывают методом от противного. Пусть \(e = \frac mn\), тогда из (7) следует, что
Домножим обе части равенства на \(n!\):
Числа \(\frac{n!}{k!} = n(n-1) \ldots (k+1)\) целые при всех \(k\) от \(0\) до \(n\), стало быть, их сумма \(\sum\limits_{k=0}^n \frac {n!}{k!}\) тоже целая. Число \(m\cdot (n-1)!\) также целое, а вот число \(\frac{\theta_n}{n}\) — как-то не очень, хотя должно быть таковым исходя из равенства (8). Полученное противоречие доказывает теорему.
Число \(e\) в виде цепной дроби#
Эйлер также нашёл разложение числа \(e\) в цепную (непрерывную) дробь
Более компактная запись того же самого: \(e = [2; 1, 2, 1, 1, 4, 1, 1, 6, 1 \dots]\).
Что ещё за цепные дроби?
Возьмём некоторое действительное число \(x\) и выделим у него целую часть:
Заметим, что \(0\leqslant x_1 < 1\) (это дробная часть \(x\)). Если \(x_1=0\), то число \(x\) оказалось целым и процесс закончен. В противном случае
Далее применяем ту же процедуру к числу \(\frac 1{x_1} > 1\): выделяем целую часть \(a_1 = \left\lfloor \frac 1{x_1} \right\rfloor \geqslant 1\), обозначаем \(x_2 = \frac 1{x_1} - a_1\), и переписываем (10) в виде
При \(x_2 > 0\) процесс снова можно продолжить по той же схеме. После \(n\) шагов таких вычислений получаем представление
Если \(x_{n+1} = 0\), то процесс завершается; соответствующая конечная цепная дробь обозначается
В противном случае процесс продолжается неограниченно долго, и в итоге мы получаем разложение числа \(x\) в бесконечную цепную дробь:
Конечная цепная дробь (11) называется также подходящей дробью для цепной дроби (12). Вообще последняя строго определяется как предел последовательности подходящих дробей:
Рассмотрим несколько первых подхоящих дробей к цепной дроби (9):
\(x_0 = 2\);
\(x_1 = [2; 1] = 2 + \frac 1{1 } = 3\);
\(x_2 = [2; 1, 2] = 2 + \cfrac 1{1 + \cfrac 1{2}}\);
\(x_3 = [2; 1, 2, 1] = 2 + \cfrac 1{1 + \cfrac 1{2 + \cfrac 1{1}}}\).
Питоновская библиотека sympy содержит удобный модуль для работы с теоретико-числовыми объектами и, в частности, цепными дробями. Для вычисления следующих значений \(x_n\) воспользуемся функцией continued_fraction_reduce.
Show code cell source
from sympy.ntheory.continued_fraction import continued_fraction_reduce
e_list =[2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 12, 1]
for n in range(4, 11):
reduced_fraction = continued_fraction_reduce(e_list[:n+1])
print(f"n = {n}, x_n = {reduced_fraction} = {reduced_fraction.evalf()}")
n = 4, x_n = 19/7 = 2.71428571428571
n = 5, x_n = 87/32 = 2.71875000000000
n = 6, x_n = 106/39 = 2.71794871794872
n = 7, x_n = 193/71 = 2.71830985915493
n = 8, x_n = 1264/465 = 2.71827956989247
n = 9, x_n = 1457/536 = 2.71828358208955
n = 10, x_n = 2721/1001 = 2.71828171828172
Результаты вычислений занесём в таблицу, аналогичную таблице 1.
\(n\) |
\(x_n \text{ (frac)}\) |
\(x_n \text{ (mixed)}\) |
\(x_n \text{ (dec)}\) |
True digits |
|---|---|---|---|---|
\(4\) |
\(\frac{19}{7}\) |
\(2\frac{5}{7}\) |
\(\mathbf{2.71}428\ldots\) |
\(3\) |
\(5\) |
\(\frac{87}{32}\) |
\(2\frac{23}{32}\) |
\(\mathbf{2.718}75\) |
\(4\) |
\(6\) |
\(\frac{106}{39}\) |
\(2\frac{28}{39}\) |
\(\mathbf{2.71}7948\ldots\) |
\(3\) |
\(7\) |
\(\frac{193}{71}\) |
\(2\frac{51}{71}\) |
\(\mathbf{2.718}3098\dots\) |
\(4\) |
\(8\) |
\(\frac{1264}{465}\) |
\(2\frac{334}{465}\) |
\(\mathbf{2.7182}79569\ldots\) |
\(5\) |
\(9\) |
\(\frac{1457}{536}\) |
\(2\frac{385}{536}\) |
\(\mathbf{2.71828}3582\ldots\) |
\(6\) |
\(10\) |
\(\frac{2721}{1001}\) |
\(2\frac{719}{1001}\) |
\(\mathbf{2.718281}71828\ldots\) |
\(7\) |
Как и в случае с частичными суммами \(s_n\), точность приближения числа \(e\) подходящей дробью \(x_n\) весьма хороша уже при небольших значениях \(n\). Нарисуем графики последовательностей \(s_n\) и \(x_n\):
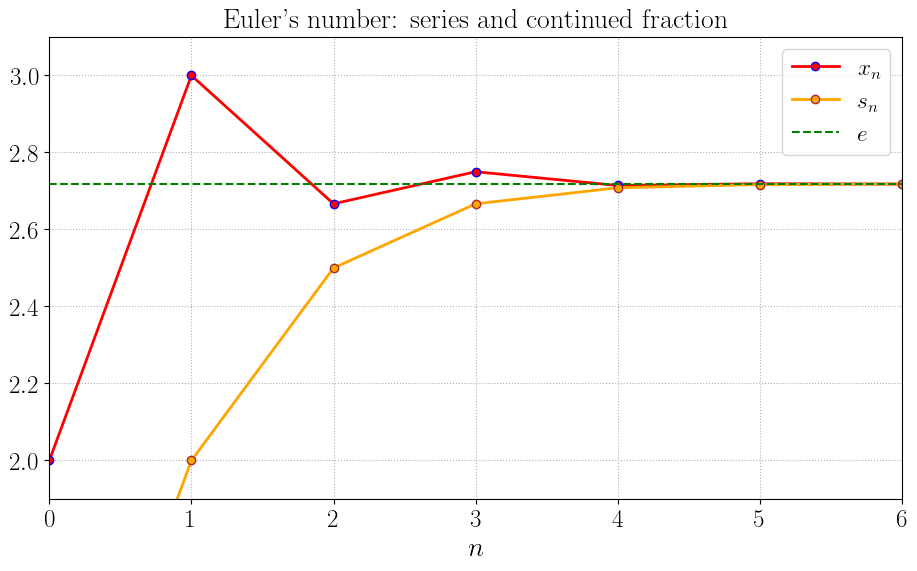
Из-за очень быстрой сходимости к числу \(e\) графики быстро сливаются, поэтому рисовать их в обычной шкале невыгодно. Для большей информативности нарисуем графики погрешностей в логарифмической шкале.
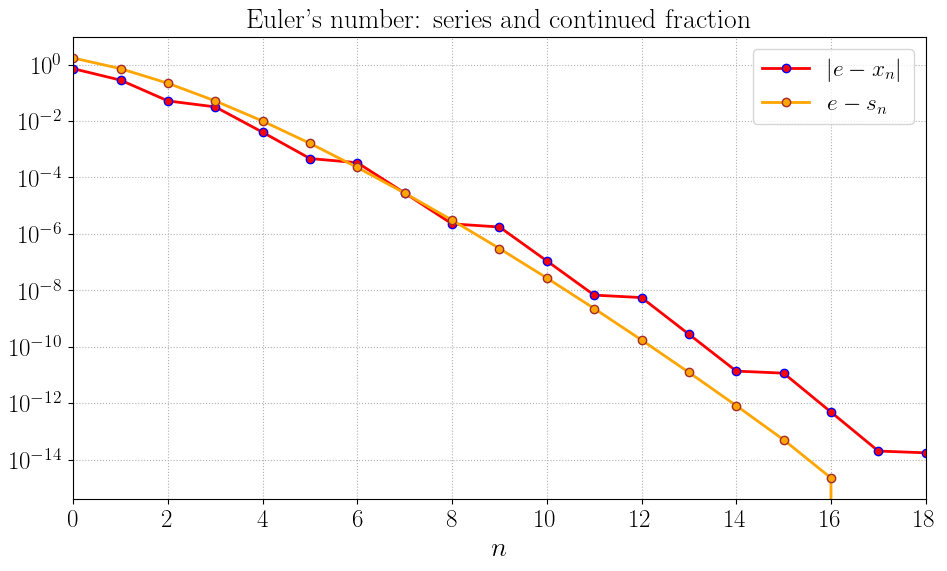
Видно, что поначалу подходящие дроби \(x_n\) дают лучшую точность, нежели частичные суммы \(s_n\), однако при \(n > 8\) ситуация меняется на противоположную (и похоже, что навсегда).
Задачи#
Пользуясь равенством \(\lim\limits_{n\to\infty} \frac 1n = 0\) и арифметическими свойствами предела, докажите, что \(\lim\limits_{n\to\infty} \frac{n^{\underline k}}{n^k} = 1\) при всех \(k\in\mathbb N\).
Вычислите сумму ряда \(\sum\limits_{n=1}^\infty \frac{n^2}{n!}\).
Докажите равенство (7):
\[ e = 1 + \frac 1{1!} + \ldots + \frac 1{n!} + \frac{\theta_n}{n!\cdot n}, \quad 0 < \theta_n < 1. \]Указание. Воспользуйтесь оценкой
\[ e - s_n = \sum\limits_{k=n+1}^\infty \frac 1{k!} = \frac 1{(n+1)!}\bigg(1 + \frac 1{n+2} + \frac 1{(n+2)(n+3)} + \ldots\bigg) < \frac 1{(n+1)!} \sum\limits_{k=0}^\infty \frac 1{(n+2)^k} \]и формулой суммы бесконечно убывающей геометрической прогрессии.
Численные расчёты показывают, что величина \(\theta_n\) из равенства (7) стремится к единице: \(\lim\limits_{n\to\infty} \theta_n = 1\). И, действительно, это следует из теоремы о двух милиционерах и неравенств \(\frac 1{(n+1)^2} < 1 - \theta_n < \frac 2{(n+1)^2}\), \(n\in \mathbb N\). Докажите эту оценку.
💻 Обозначим через \(d_n\) количество верных десятичных знаков числа \(e\), которые даёт частичная сумма \(s_n\) (см. правый столбец таблицы 1). Вычислите \(d_n\) для \(n\leqslant 100\) и постройте график этой последовательности.
💻 Сделайте то же самое, что и в предыдущей задаче, для количества верных цифр числа \(e\), вычисленных с помощью подходящих дробей цепной дроби (9) (т.е. продолжите правый столбец таблицы 2).
