Convolution of matrices

Convolution of matrices#

1-d convolution#

Convolution is a widespread operation in mathematics in different contexts.

Convolution of sequences#

The convolution of sequences \((a_n)\) and \((b_n)\) is the sequence \(a * b\) such that

(40)#\[(a * b)_n = \sum\limits_k a_k b_{n-k}\]

This formula assumes that the sequences \((a_n)\) and \((b_n)\) continue indefinitely to both sides. To calculate the convolution of finite sequences

\[ a_0, \ldots, a_{\ell-1}, \quad b_0, \ldots, b_{m-1} \]

they are padded by zeros:

\(a_k = 0\) if \(k < 0\) or \(k \geqslant \ell\);
\(b_k = 0\) if \(k < 0\) or \(k \geqslant m\).

Exercise

Let \((a_n) = (1, 2, 3)\), \((b_n) = (4, 5)\). Calculate their convolution.

Question

How many nonzero elements are there in (40) for these finite sequences?

In practice there are several reasonable strategies how to caclulate convolutions.

full: find \((a * b)_n\) for all \(n\) such that

\[ a_0, \ldots, a_{\ell-1} \text{ and } \quad b_{n-m+1}, \ldots, b_{n} \]

have at least one nonzero intersection, the shape of \((a * b)_n\) is \(\ell + m - 1\);
same: the convolution has the same shape as the largest input sequence, the shape of \(c_n\) is \(\max\{\ell, m\}\);
valid: the convolution product is only given for points where the sequences overlap completely, the shape of \(c_n\) is \(\max\{\ell, m\} - \min\{\ell, m\} + 1\).

Convolution in NumPy#

Use np.convolve:

import numpy as np

a = np.array([1, 2, 3])
b = np.array([4, 5])
print("Full:", np.convolve(a, b, mode='full'))
print("Same:", np.convolve(a, b, mode='same'))
print("Valid:", np.convolve(a, b, mode='valid'))

Full: [ 4 13 22 15]
Same: [ 4 13 22]
Valid: [13 22]

Cross correlation#

This is a very similar operation to convolution. The cross correlation of sequences \((a_n)\) and \((b_n)\) is a sequence \((c_n)\) such that

(41)#\[c_n = \sum\limits_k a_{n+k} b_k\]

np.correlate calculates the cross correlation of two arrays. The meaning of the parameters full, same, valid is analogous to those of np.convolve:

print("Full:", np.correlate(a, b, mode='full'))
print("Same:", np.correlate(a, b, mode='same'))
print("Valid:", np.correlate(a, b, mode='valid'))

Full: [ 5 14 23 12]
Same: [ 5 14 23]
Valid: [14 23]

Question

How to express cross correlation it terms of convolution?

Answer

Denote \((x^-_n)\) the flipped sequence: \(x^-_n = x_{-n}\). Now \(c_n\) from (41) is

\[ c_n = \sum\limits_k a^-_{-n-k} b_k = (a^- * b)_{-n}=(a^- * b)^-_n. \]

Alternatively, we can write it as

\[ c_n = \sum\limits_k a_{n+k} b^-_{-k} = \sum\limits_k a_j b^-_{n-j} = (a * b^-)_n. \]

Thus, the cross correlation can be represented as a convolution of two initial sequences exactly one of which is flipped.

print("Convolution:", np.convolve(a, b, mode='full'))
print("Correlation, flip first:", np.correlate(a[::-1], b, mode='full')[::-1])
print("Correlation, flip second:", np.correlate(a, b[::-1], mode='full'))

Convolution: [ 4 13 22 15]
Correlation, flip first: [ 4 13 22 15]
Correlation, flip second: [ 4 13 22 15]

2-d convolution#

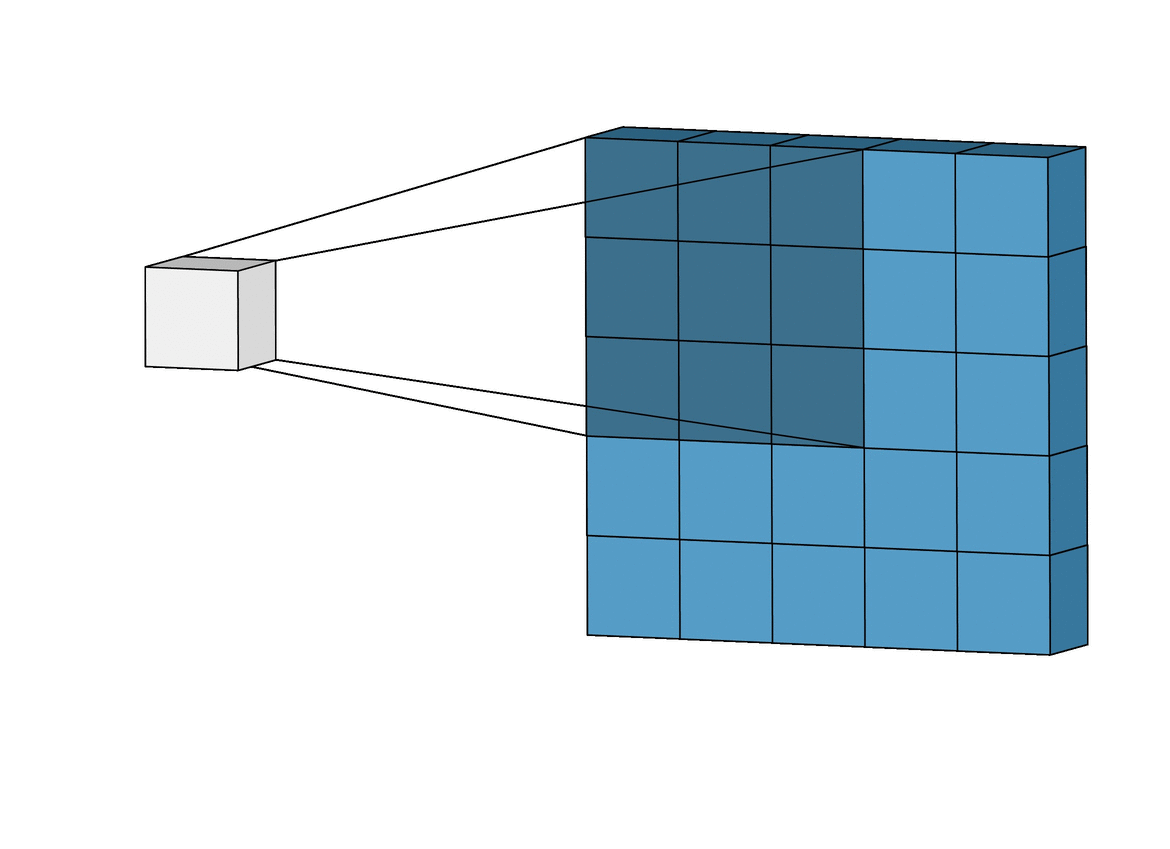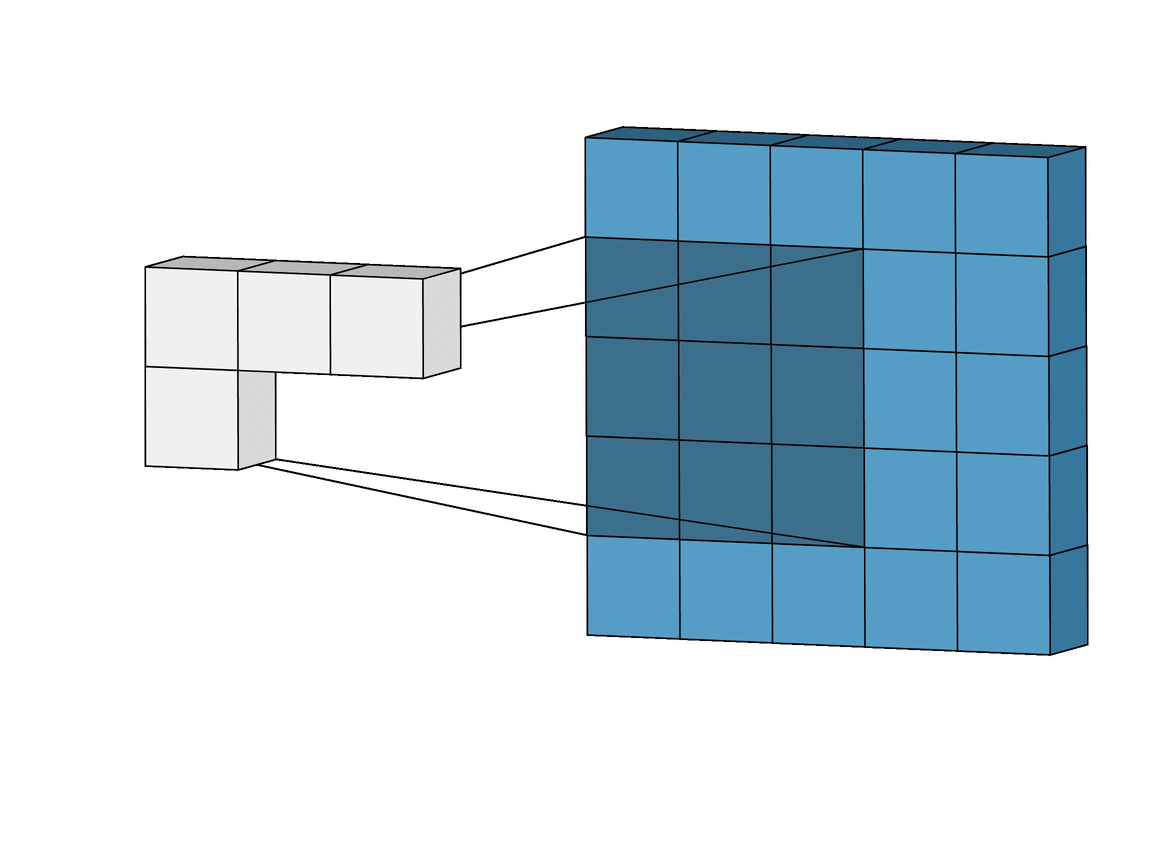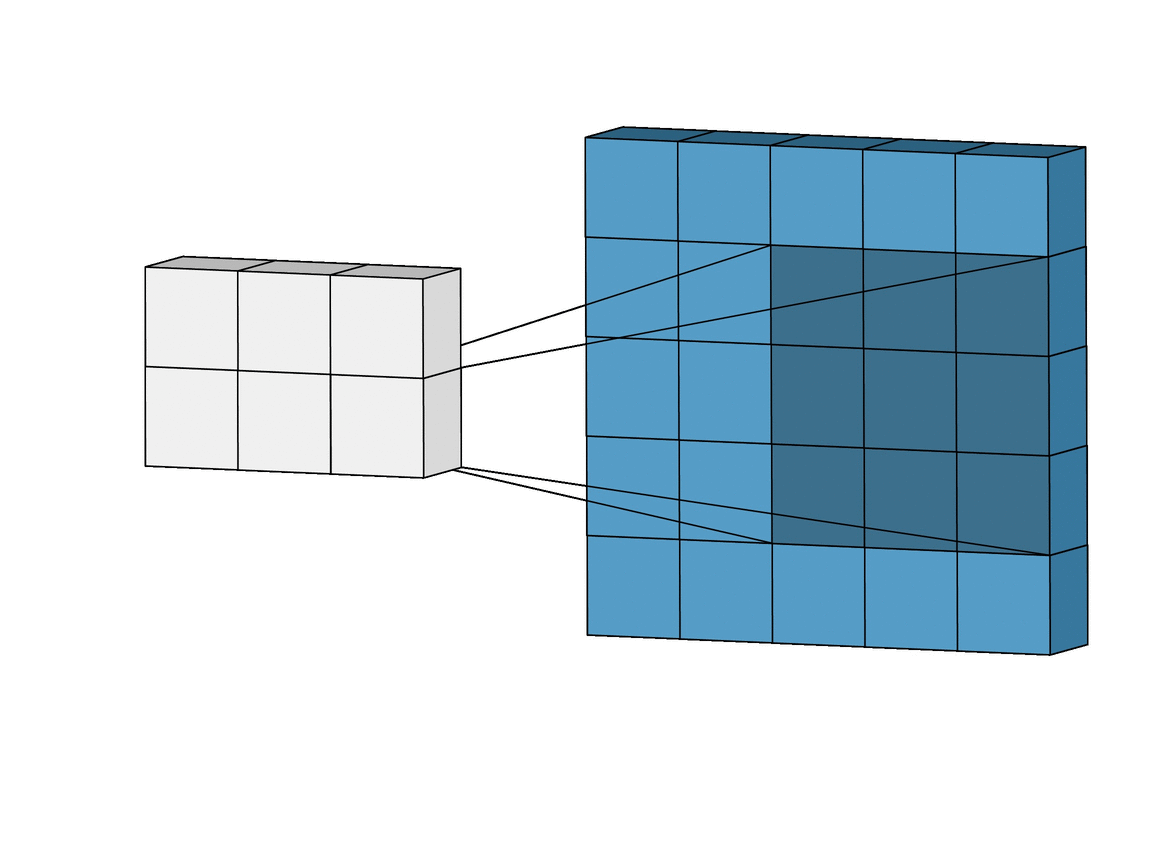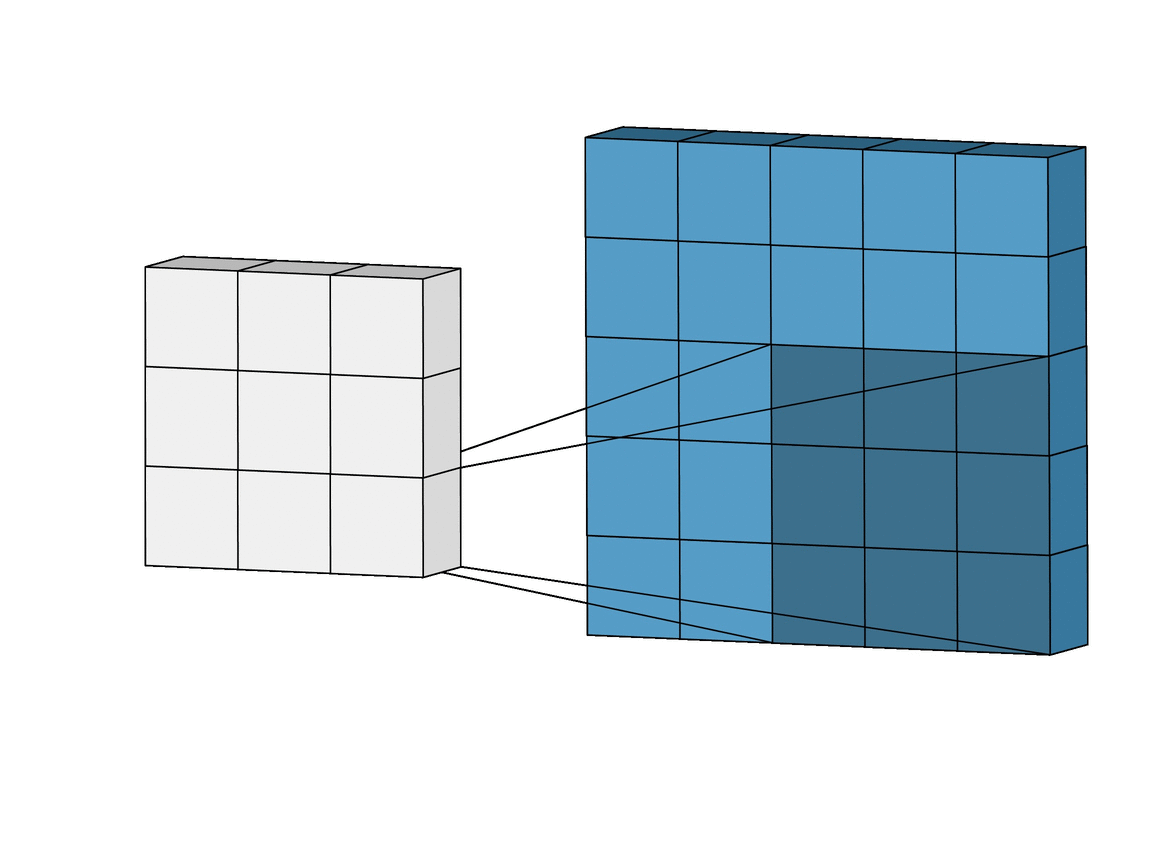
https://miro.medium.com/v2/resize:fit:1358/1*Fw-ehcNBR9byHtho-Rxbtw.gif

Two-dimensinonal convolutions are similar to convolutions of sequences. For two matrices \(\boldsymbol A\) and \(\boldsymbol B\) their convolution is defined a

\[ (\boldsymbol A * \boldsymbol B)_{k\ell} = \sum\limits_i \sum \limits_j A_{ij} B_{k-i, \ell-j}. \]

Once again matrices are padded by zeros outside their shape.

Exercise

Let

\[\begin{split} \boldsymbol A = \begin{pmatrix} 0 & 1 & 2 & 3 \\ 4 & 5 & 6 & 7 \\ 8 & 9 & 10 & 11 \end{pmatrix}, \quad \boldsymbol B = \begin{pmatrix} 2 & 0 \\ 1 & -1 \end{pmatrix}. \end{split}\]

Calculate \(\boldsymbol A * \boldsymbol B\) in all three modes: full, same, valid.

Now check these results via scipy.signal.convolve2d:

What about pyTorch? Note that to proceed in the full mode we can pad \(\boldsymbol A\) by one zero from each side.

Warning

The outputs of scipy.signal.convolve2d and torch.nn.conv2dlook different. What is the reason of it?

Answer

Pytorch calculates not convolution but cross correlation:

\[ (\boldsymbol A \circledast \boldsymbol B)_{k\ell} = \sum\limits_i \sum \limits_j A_{ij} B_{k+i, \ell+j}. \]

Image convolution#

Grayscale images of size \(H\times W\) are stored as matrices of shape \(H\times W\). Here is an example:

import numpy as np
import matplotlib.pyplot as plt 
import requests
import io
from PIL import Image

%config InlineBackend.figure_format = 'svg'

r = requests.get('https://github.com/probml/probml-data/blob/main/data/clown.png?raw=true', stream=True)
img = Image.open(io.BytesIO(r.content))
X = np.array(img) / 255
plt.xticks([])
plt.yticks([])
plt.imshow(X, cmap="gray");

../_images/74478c3d8c65ccccde57b8156740b0bfea849a0960ea301778a98d359b9876e5.svg

The shape is \(H\times W = 200\times 320\):

X.shape

(200, 320)

Convolving with kernel \(K = \frac 1{n^2} \boldsymbol 1_{n\times n}\) averages the values of each pixel with its neigbours, so the image becomes blurred:

def blur_image(X, n):
    kernel = np.ones((n, n)) / n**2
    blurred_image = convolve2d(X, kernel, mode="same")
    plt.xticks([])
    plt.yticks([])
    plt.imshow(blurred_image, cmap="gray");

\(n=3\):

blur_image(X, 3)

../_images/48fe2a6694747cd62c182a6fcddf019aac71bfa066c1e34df92431b86dffcd15.svg

\(n = 8\):

blur_image(X, 8)

../_images/a95c03dda51dfcfbb5f2dae529c9e91db98cd690e4df0539366b720035f77943.svg

Now what if we convolve the image with kernel

\[\begin{split} \begin{pmatrix} -1 & -1 & -1 \\ -1 & 8 & -1 \\ -1 & -1 & -1 \end{pmatrix}? \end{split}\]

Stride#

Sometimes convolution are used with stride greater than one. To calculate the next element of the convolution the filter is moved by stride units. Here is a gif of a convolution with stride equal to \(2\):

Exercise

Calculate both convolution and cross correlation for the same matrices

\[\begin{split} \boldsymbol A = \begin{pmatrix} 0 & 1 & 2 & 3 \\ 4 & 5 & 6 & 7 \\ 8 & 9 & 10 & 11 \end{pmatrix}, \quad \boldsymbol B = \begin{pmatrix} 2 & 0 \\ 1 & -1 \end{pmatrix}. \end{split}\]

with stride \(2\) in mode full.

Check with pyTorch:

Dilation#

The kernel can be multiplied not only to contiguous pieces of input, they can be separated by several cells. This is regulated by the dilation parameter. Here is a gif of a convolution with dilation equal to \(2\):

Exercise

Calculate both convolution and cross correlation for the same matrices

\[\begin{split} \boldsymbol A = \begin{pmatrix} 0 & 1 & 2 & 3 \\ 4 & 5 & 6 & 7 \\ 8 & 9 & 10 & 11 \end{pmatrix}, \quad \boldsymbol B = \begin{pmatrix} 2 & 0 \\ 1 & -1 \end{pmatrix}. \end{split}\]

with dilation \(2\) in mode same.

Check with pyTorch:

conv = nn.Conv2d(1, 1, 3, bias=False, dilation=2, padding='same')
conv.weight = nn.parameter.Parameter(torch.FloatTensor(B[None, None, :, :]))
print(conv(torch.FloatTensor(A[None, None, :, :])).detach().numpy().squeeze())

[[-5. -2. -2.  6.]
 [-9. -2.  0. 14.]
 [ 0.  8. 10. 12.]]

Output shape formula#

Convolutions have a lot of parameters. How do they affect the shape of the convolved image?

Suppose that

input image has shape \(H\times W\);
kernel has shape \(h\times w\);
the imput image is padded by \(p\) zeros from each side (\(p \geqslant 0\));
stride is \(s\) (by default \(s=1\));
dilation is \(d\) (by default \(d=1\)).

Then the height of the convolved image is

\[ H_{\mathrm{out}} = \bigg\lfloor \frac{H + 2p - 1 - d(h-1)}s + 1 \bigg\rfloor \]

and the width is

\[ W_{\mathrm{out}} = \bigg\lfloor \frac{W + 2p - 1 - d(w-1)}s + 1 \bigg\rfloor. \]

For example, if \(s=d=1\), \(h=w = 2k+1\), \(p=k\), then

\[ H_{\mathrm{out}} = H + 2k - 1 - 2k + 1 = H, \quad W_{\mathrm{out}} = W + 2k - 1 - 2k + 1 = W. \]

This is how same mode is achieved.

Convolution of matrices

Contents

Convolution of matrices#

1-d convolution#

Convolution of sequences#

Convolution in NumPy#

Cross correlation#

2-d convolution#

Image convolution#

Stride#

Dilation#

Output shape formula#