Markov Decision Process (MDP)

MDP-1

\((\mathcal S, \mathcal A, p, \gamma)\):

• \(\mathcal S\) is a set of all possible states

• \(\mathcal A\) — set of actions (can depend on \(s \in\mathcal S\))

• \(p(r, s' \vert s, a)\) — joint probability distribution of reward \(r\) and next state \(s'\) given state \(s\) and action \(a\)

• \(\gamma \in [0,1]\) — discount factor

MDP-2

\((\mathcal S, \mathcal A, p, \mathcal R, \gamma)\):

• \(\mathcal S\) is a set of all possible states

• \(\mathcal A\) — set of actions

• \(p(s' \vert s, a)\) is the probability of transitioning to \(s'\), given a state \(s\) and action \(a\)

• \(\mathcal R \colon \mathcal S \times \mathcal A \to \mathbb R\) — expected reward: \(\mathcal R(s, a) = \mathbb E[R \vert s, a]\)

• \(\gamma \in [0,1]\) — discount factor

Question

How to obtain MDP-2 from MDP-1?

Answer

\[ \mathcal R(s, a) = \mathbb E[R \vert s, a] = \sum\limits_{r, s'} rp(r, s' | s, a), \quad p(s' | s, a) = \sum\limits_{r} p(r, s' | s, a) \]

Value function

Value (expected return) of following policy \(\pi\) from state \(s\):

\[ v_\pi(s) = \mathbb E_\pi[G_t \vert S_t = s] \]

Bellman expectation equality for \(v_\pi(s)\)

MDP-1:

\[ v_\pi(s) = \sum\limits_{a\in\mathcal A} \pi(a\vert s) \sum\limits_{r, s'}p(r, s'\vert s, a)(r + \gamma v_{\pi}(s')) \]

MDP-2:

\[ v_\pi(s) = \sum\limits_{a\in\mathcal A} \pi(a\vert s) \Big(\mathcal R(s, a) + \gamma \sum\limits_{s'}p(s'\vert s, a) v_{\pi}(s')\Big) \]

Note that we need to fix some policy \(\pi\) in this equation.

Exericse

Check that Bellman expectation equality holds for the center state of the gridworld.

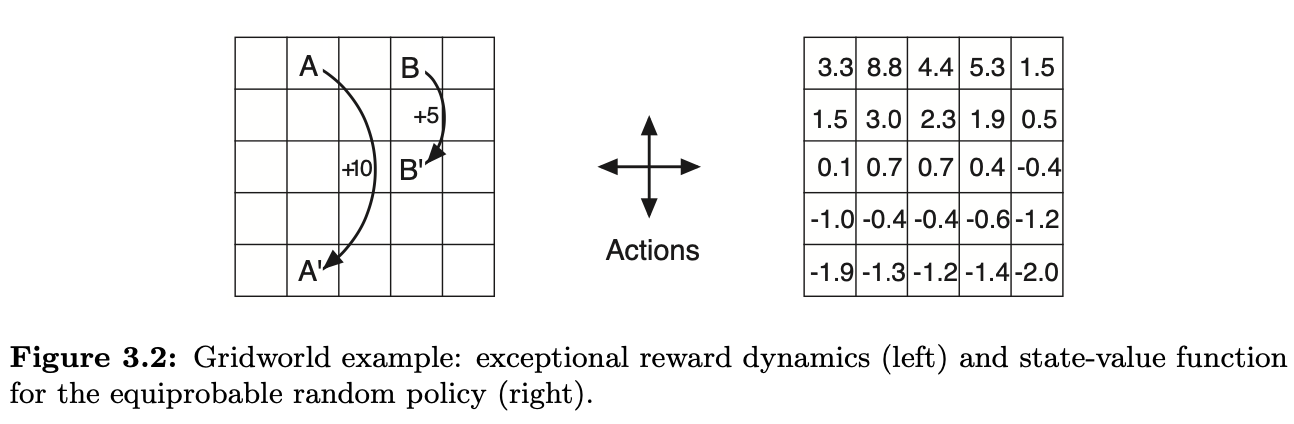
grid = GridWorld(5, 5, [(1, 21, 10), (3, 13, 5)])
values = grid.bellman_solution()
sns.heatmap(values, cmap='RdBu', annot=True, fmt=".3f");

Action-value function

Value (expected return) of following policy \(\pi\) after committing action \(a\) state \(s\):

\[ q_\pi(s, a) = \mathbb E_\pi[G_t \vert S_t = s, A_t = a] \]

Question

How to write \(v_\pi(s)\) in terms of \(q_\pi(s, a)\)?

Answer

\[ v_\pi(s) = \sum\limits_a \pi(a\vert s) q_\pi(s, a) \]

Bellman expectation equality for \(q_\pi(s, a)\)

MDP-1:

\[ q_\pi(s,a) = \sum\limits_{r, s'}p(r, s'\vert s, a)(r + \gamma v_{\pi}(s')) \]

Since \(v_\pi(s) = \sum\limits_{a} \pi(a\vert s) q_\pi(s, a)\), we obtain

\[ q_\pi(s,a) = \sum\limits_{r, s'}p(r, s'\vert s, a)\Big(r + \gamma \sum\limits_{a'}\pi(a'\vert s') q_\pi(s', a')\Big) \]

MDP-2:

\[ q_\pi(s,a) = \mathcal R(s, a) + \gamma\sum\limits_{s'}p(s'\vert s, a)\sum\limits_{a'}\pi(a'\vert s') q_\pi(s', a') \]

Once again the equation stands for some fixed policy \(\pi\)

Optimal policy

Optimal policy \(\pi_*\) is the one with the largest \(v_\pi(s)\):

\[ v_*(s) = \max\limits_\pi v_\pi(s), \quad v_*(s) = v_{\pi_*}(s) \]

\[ q_*(s, a) = \max\limits_\pi q_\pi(s, a), \quad q_*(s, a) = q_{\pi_*}(s, a) \]

Note that both \(v_*(s)\) and \(q_*(s, a)\) do not depend on \(\pi\) anymore

If we now optimal action-value function \(q_*(s, a)\), then the optimal deterministic policy can be found as

\[\begin{split} \pi_*(a\vert s) = \begin{cases} 1, & a = \arg\max\limits_a q_*(s, a), \\ 0, & \text{otherwise}. \end{cases} \end{split}\]

Bellman optimality equality for \(v_*(s)\)

MDP-1:

\[ v_*(s) = \max\limits_a q_*(s, a) = \max\limits_a\sum\limits_{r, s'}p(r, s'\vert s, a)(r + \gamma v_*(s')) \]

MDP-2:

\[ v_*(s) = \max\limits_a \Big\{\mathcal R(s, a) + \gamma\sum\limits_{s'}p(s'\vert s, a)v_*(s')\Big\} \]

Bellman optimality equality for \(q_*(s, a)\)

MDP-1:

\[ q_*(s, a) = \sum\limits_{r, s'}p(r, s'\vert s, a)\big(r + \gamma \max\limits_{a'} q_*(s', a')\big) \]

MDP-2:

\[ q_*(s, a) = \mathcal R(s, a) + \gamma\sum\limits_{s'}p(s'\vert s, a) \max\limits_{a'} q_*(s', a') \]

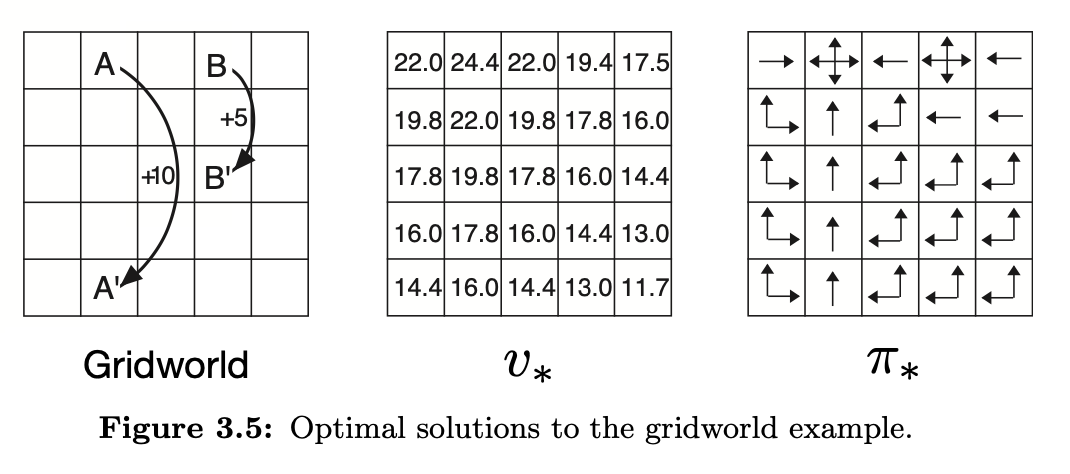
Exercise

Compute \(v_*\) of the best state \(A\).

10 / (1- 0.9**5)

24.419428096993972

Value iteraion

1. Initialize \(v_i(s)=0\), for all \(s \in \mathcal S\)

2. While \(\|v_{i+1} - v_i\| > \varepsilon\):

3. \(\quad v_{i+1}(s) = \max\limits_a \sum\limits_{r, s'} p(r, s' | s,a)\big(r + \gamma v_{i}(s')\big)\), \(s \in \mathcal S\)

After \(n\) iterations \(v_n(s) \approx v_*(s)\) for all \(s\in\mathcal S\), so the optimal policy is now evaluated as

\[ \pi_*(s) = \arg\max\limits_a \sum\limits_{r, s'} p(r, s' | s,a)\big(r + \gamma v_*(s')\big) \]

Q. How to update the value function in MDP-2?

\(\quad v_{i+1}(s) = \max\limits_a \big\{\mathcal R(s, a) +\gamma\sum\limits_{s'} p(s' | s,a) v_{i}(s')\big\}\)

Apply the value iteration methods to the gridworld environment:

grid = GridWorld(5, 5, [(1, 21, 10), (3, 13, 5)])
for i in range(1000):
    diff = grid.update_state_values()
    print(f"diff at iteration {i}: {diff:.6f}")
    if diff < 1e-3:
        break

diff at iteration 0: 11.180340
diff at iteration 1: 16.837458
diff at iteration 2: 15.153712
diff at iteration 3: 14.390083
diff at iteration 4: 13.201365
diff at iteration 5: 11.359212
diff at iteration 6: 10.087099
diff at iteration 7: 8.899113
diff at iteration 8: 8.128209
diff at iteration 9: 7.426842
diff at iteration 10: 6.520376
diff at iteration 11: 5.832493
diff at iteration 12: 5.165771
diff at iteration 13: 4.786819
diff at iteration 14: 4.422070
diff at iteration 15: 3.967694
diff at iteration 16: 3.580832
diff at iteration 17: 3.102996
diff at iteration 18: 2.886449
diff at iteration 19: 2.703556
diff at iteration 20: 2.447296
diff at iteration 21: 2.182663
diff at iteration 22: 1.821722
diff at iteration 23: 1.697455
diff at iteration 24: 1.627680
diff at iteration 25: 1.530449
diff at iteration 26: 1.368849
diff at iteration 27: 1.087588
diff at iteration 28: 1.036305
diff at iteration 29: 1.036065
diff at iteration 30: 1.016825
diff at iteration 31: 0.915050
diff at iteration 32: 0.679617
diff at iteration 33: 0.618063
diff at iteration 34: 0.621914
diff at iteration 35: 0.613145
diff at iteration 36: 0.551831
diff at iteration 37: 0.405511
diff at iteration 38: 0.364960
diff at iteration 39: 0.367234
diff at iteration 40: 0.362056
diff at iteration 41: 0.325851
diff at iteration 42: 0.239450
diff at iteration 43: 0.215505
diff at iteration 44: 0.216848
diff at iteration 45: 0.213791
diff at iteration 46: 0.192412
diff at iteration 47: 0.141393
diff at iteration 48: 0.127254
diff at iteration 49: 0.128047
diff at iteration 50: 0.126241
diff at iteration 51: 0.113617
diff at iteration 52: 0.083491
diff at iteration 53: 0.075142
diff at iteration 54: 0.075610
diff at iteration 55: 0.074544
diff at iteration 56: 0.067090
diff at iteration 57: 0.049301
diff at iteration 58: 0.044371
diff at iteration 59: 0.044647
diff at iteration 60: 0.044018
diff at iteration 61: 0.039616
diff at iteration 62: 0.029112
diff at iteration 63: 0.026200
diff at iteration 64: 0.026364
diff at iteration 65: 0.025992
diff at iteration 66: 0.023393
diff at iteration 67: 0.017190
diff at iteration 68: 0.015471
diff at iteration 69: 0.015567
diff at iteration 70: 0.015348
diff at iteration 71: 0.013813
diff at iteration 72: 0.010151
diff at iteration 73: 0.009136
diff at iteration 74: 0.009192
diff at iteration 75: 0.009063
diff at iteration 76: 0.008157
diff at iteration 77: 0.005994
diff at iteration 78: 0.005394
diff at iteration 79: 0.005428
diff at iteration 80: 0.005352
diff at iteration 81: 0.004816
diff at iteration 82: 0.003539
diff at iteration 83: 0.003185
diff at iteration 84: 0.003205
diff at iteration 85: 0.003160
diff at iteration 86: 0.002844
diff at iteration 87: 0.002090
diff at iteration 88: 0.001881
diff at iteration 89: 0.001893
diff at iteration 90: 0.001866
diff at iteration 91: 0.001679
diff at iteration 92: 0.001234
diff at iteration 93: 0.001111
diff at iteration 94: 0.001118
diff at iteration 95: 0.001102
diff at iteration 96: 0.000992

sns.heatmap(grid.values.reshape(5,5), cmap='RdBu', annot=True, fmt=".3f");

Policy iteration

Initialize \(\pi_0\) (random or fixed). For \(n=0, 1, 2, \dots\)

• Compute the value function \(v_{\pi_{n}}\) by solving Bellman expectation linear system

• Compute the value-action function \(q_{\pi_{n}}(s, a) = \sum\limits_{r, s'} p(r, s' | s,a)\big(r + \gamma v_{\pi_{n}}(s')\big)\)

• Compute new policy \(\pi_{n+1}(s) = \operatorname*{argmax}\limits_a q_{\pi_{n}}(s,a)\)

Q. Rewrite update of \(q_\pi\) it terms of MDP-2 framework.

\(q_{\pi_{n}}(s, a) = \mathcal R(s,a) + \gamma\sum\limits_{s'} p(s' | s,a)v_{\pi_{n}}(s')\)