Regularization#

If the columns of the feature matrix \(\boldsymbol X\) are highly correlated, the weights of linear regression could be unstable and excessively large. To fight this, a regularization term is added to the MSE loss function.

Ridge regression#

To penalize weights that are too large in magnitude, add a multiple of

\[ \Vert \boldsymbol w \Vert_2^2 = \boldsymbol w^\top \boldsymbol w = \sum\limits_{j=1}^d w_j^2 \]

to RSS; the new loss function is

\[ \mathcal L(\boldsymbol w) = \Vert \boldsymbol y - \boldsymbol{Xw}\Vert_2^2 + C\Vert \boldsymbol w \Vert_2^2, \quad C>0. \]

To find the optimal weights, one need to solve the equation \(\nabla_{\boldsymbol w} \mathcal L(\boldsymbol w) = \boldsymbol 0\).

Since \(\nabla_{\boldsymbol w}(\Vert \boldsymbol w \Vert_2^2) = 2\boldsymbol w\), we receive one additional term to (22):

\[ \boldsymbol X^\top \boldsymbol X\boldsymbol w - \boldsymbol X^\top \boldsymbol y + C\boldsymbol w = \boldsymbol 0. \]

From here we obtain

\[ \widehat{\boldsymbol w} = (\boldsymbol X^\top \boldsymbol X + C\boldsymbol I)^{-1} \boldsymbol X^\top \boldsymbol y. \]

Note that this is equal to (23) if \(C=0\). Ridge regression also allows to avoid inverting of a singular matrix.

Once again take the Boston dataset, and try ridge regression on it:

from sklearn.linear_model import Ridge
import numpy as np
import pandas as pd

boston = pd.read_csv("../ISLP_datsets/Boston.csv")

target = boston['medv']
train = boston.drop(['medv', "Unnamed: 0"], axis=1)
ridge = Ridge()
ridge.fit(train, target)
print("intercept:", ridge.intercept_)
print("coefficients:", ridge.coef_)
print("r-score:", ridge.score(train, target))
print("MSE:", np.mean((ridge.predict(train) - target) ** 2))

intercept: 36.66359752181638
coefficients: [-1.18324104e-01  4.80549483e-02 -1.78537994e-02  2.70383610e+00
 -1.14024737e+01  3.70139930e+00 -2.75076805e-03 -1.38242357e+00
  2.71825248e-01 -1.33051618e-02 -8.55687104e-01 -5.62037458e-01]
r-score: 0.73233360340788
MSE: 22.59627839822696

LASSO regression#

The only difference with ridge regression is that \(L^1\)-norm is used for the regularization term:

\[ \Vert \boldsymbol w \Vert_1 = \sum\limits_{j=1}^d \vert w_j \vert. \]

Accordingly, the loss function switches to

\[ \mathcal L(\boldsymbol w) = \Vert \boldsymbol y - \boldsymbol{Xw}\Vert_2^2 + C\Vert \boldsymbol w \Vert_1, \quad C>0, \]

and the optimal weights \(\widehat w\) are the solution of the optimization task

(25)#\[\Vert \boldsymbol y - \boldsymbol{Xw}\Vert_2^2 + C\Vert \boldsymbol w \Vert_1 \to \min\limits_{\boldsymbol w}.\]

Note

LASSO stands for Least Absolute Shrinkage and Selection Operator

Important property of Lasso regression is feature selection. Usually some coorditates of the optimal vector of weights \(\widehat {\boldsymbol w}\) turn out to be zero. A famous picture from [Murphy, 2022]:

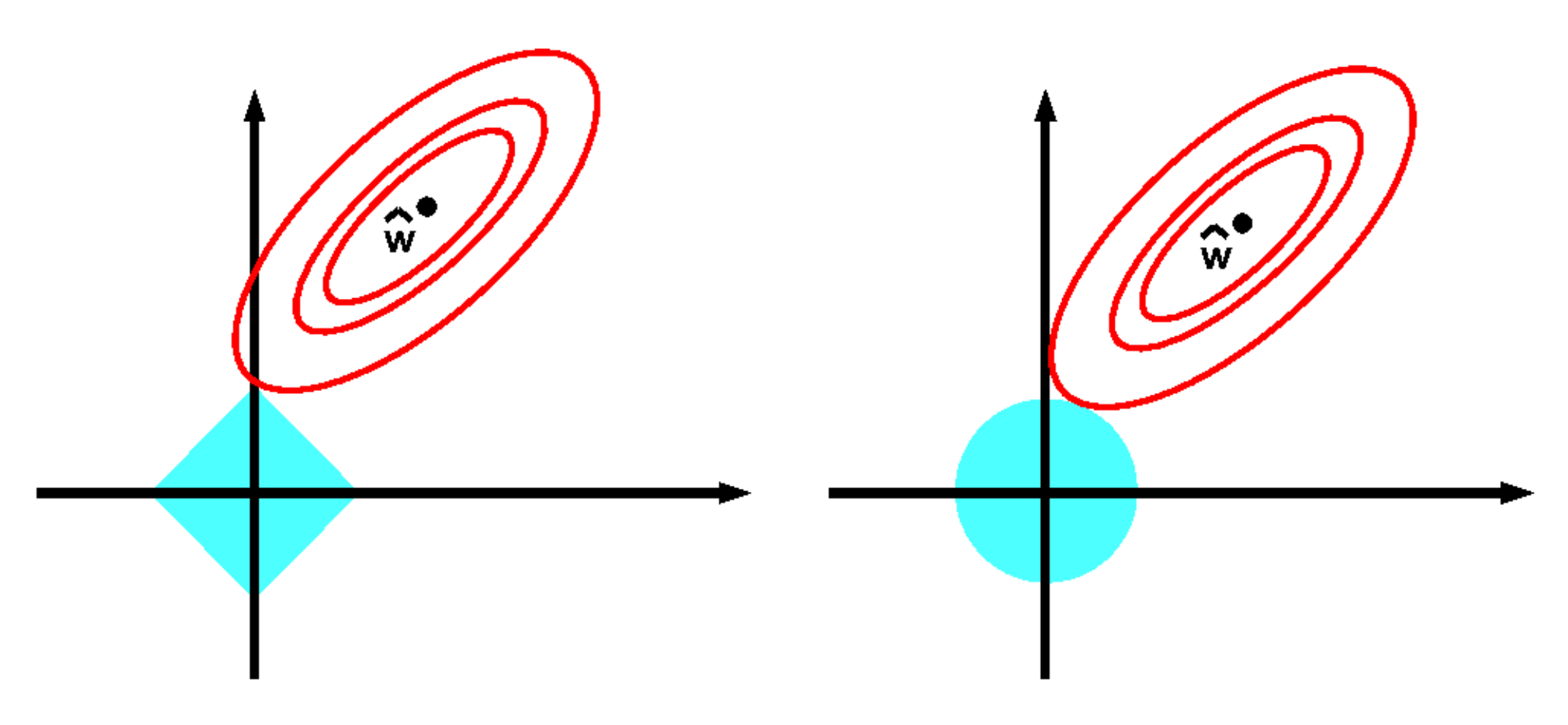
../_images/Figure_11.8.png

Advantages of LASSO

  • strong theoretical guarantees

  • sparse solution

  • feature selection

However, there is no closed-form solution of (25).

Empirical recipe to provide better prediction performance:

  • first, perform variable selection using LASSO;

  • Second, re-estimate model parameters with selected variables using Ridge regression.

See how Lasso regression works on Boston dataset:

from sklearn.linear_model import Lasso

lasso = Lasso()
lasso.fit(train, target)
print("intercept:", lasso.intercept_)
print("coefficients:", lasso.coef_)
print("r-score:", lasso.score(train, target))
print("MSE:", np.mean((lasso.predict(train) - target) ** 2))

intercept: 44.98510958345055
coefficients: [-0.07490856  0.05004565 -0.          0.         -0.          0.83244563
  0.02266242 -0.66083402  0.25070221 -0.01592473 -0.70206981 -0.7874801 ]
r-score: 0.6745576822708007
MSE: 27.47369601713281

Three coeffitients vanished, namely indus, chas, nox:

boston.columns[3:6]

Index(['indus', 'chas', 'nox'], dtype='object')

Elastic net#

Elasitc net is a hybrid between lasso and ridge regression. This corresponds to minimizing the following objective:

\[ \mathcal L(\boldsymbol w) = \Vert \boldsymbol y - \boldsymbol{Xw}\Vert_2^2 + C_1\Vert \boldsymbol w \Vert_1 + C_2\Vert \boldsymbol w \Vert_2^2, \quad C_1, C_2>0. \]

Motivation

  • If there is a group of variables with high pairwise correlations, then the LASSO tends to select only one variable from the group and does not care which one is selected

  • It has been empirically observed that the prediction performance of the LASSO is dominated by ridge regression

  • Elastic Net includes regression, variable selection, with the capacity of selecting groups of correlated variables

  • Elas9tic Net is like a stretchable fishing net that retains ‘all the big fish’ ([Zou and Hastie, 2003])

Applied to Boston dataset, it zeroes two coefficients:

from sklearn.linear_model import ElasticNet

en = ElasticNet()
en.fit(train, target)
print("intercept:", en.intercept_)
print("coefficients:", en.coef_)
print("r-score:", en.score(train, target))
print("MSE:", np.mean((en.predict(train) - target) ** 2))

intercept: 45.68409537995804
coefficients: [-0.09222698  0.05335925 -0.02011639  0.         -0.          0.89077605
  0.02193951 -0.7586982   0.28439842 -0.01686424 -0.72640381 -0.77837394]
r-score: 0.679766219677128
MSE: 27.033993601067873

Exercises#

  1. Prove that the matrix \(\boldsymbol X^\top \boldsymbol X + C\boldsymbol I\) is invertible for all \(C >0\).

TODO

  • Add some simple quizzes

  • Add more datasets

  • Show the advantages of different typse of regularization on real and/or simulated datasets

  • Describe Ridge(), Lasso(), ElasticNet() more thoroughly