Model selection

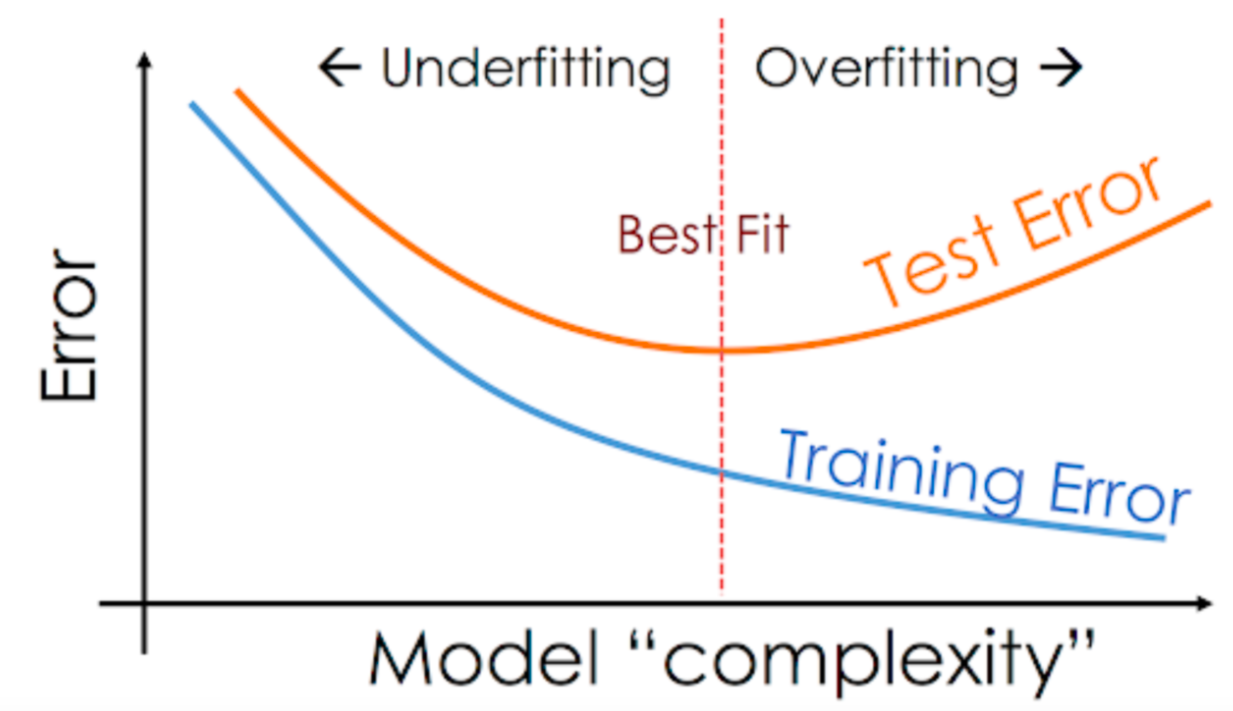
Underfitting

• the model is too simple

• the number of parameters is too low

Overfitting

• the model is too complex

• the number of parameters is too large

Train and test

The common way to reveal overfitting is to use train and test datasets.

• training dataset \(\mathcal D_{\mathrm{train}} = (\boldsymbol X_{\mathrm{train}}, \boldsymbol y_{\mathrm{train}})\) is used on learning stage:

\[ \mathcal L_{\mathrm{train}}(\boldsymbol \theta) = \frac 1{N_{\mathrm{train}}}\sum\limits_{(\boldsymbol x_i, y_i) \in \mathcal D_{\mathrm{train}}} \ell(y_i, f_{\boldsymbol \theta}(\boldsymbol x_i)) \to \min\limits_{\boldsymbol \theta} \]

• test dataset \(\mathcal D_{\mathrm{test}} = (\boldsymbol X_{\mathrm{test}}, \boldsymbol y_{\mathrm{test}})\) used for evlaluation of model’s quality:

\[ \mathcal L_{\mathrm{test}}(\boldsymbol \theta) = \frac 1{N_{\mathrm{test}}}\sum\limits_{(\boldsymbol x_i, y_i) \in \mathcal D_{\mathrm{test}}} \ell(y_i, f_{\boldsymbol \theta}(\boldsymbol x_i)) \]

A classical example

• Ground truth: \(y(x) = \frac 1{1 + 25x^2}\), \(-2\leqslant x \leqslant 2\)

• Polynomial regression model: \(f_{\boldsymbol \theta}(x) = \sum\limits_{k=0}^n \theta_k x^k\)

• Training set: \(X = \Big\{x_i = 4\frac{i-1}{N-1} - 2\Big\}_{i=1}^N\)

• Test set: \(\tilde X = \Big\{\tilde x_i = 4\frac{i-0.5}{N-1} - 2\Big\}_{i=1}^{N-1}\)

• Loss function — MSE:

  \[ \mathcal L_{\mathrm{train}}(\boldsymbol \theta, X) = \frac 1N \sum\limits_{i=1}^N (f_{\boldsymbol \theta}(x_i) - y_i)^2 \to \min\limits_{\boldsymbol \theta} \]

• What is happening with test loss

  \[ \mathcal L_{\mathrm{test}}(\boldsymbol \theta, \tilde X) = \frac 1N \sum\limits_{i=1}^N (f_{\boldsymbol \theta}(\tilde x_i) - \tilde y_i)^2 \]

as \(n\) grows?

The overfitting is a big problem in ML because an overfitted model makes poor predictions. The first signal of the overfitting: \(\mathcal L_{\mathrm{train}} \ll \mathcal L_{\mathrm{test}}\).

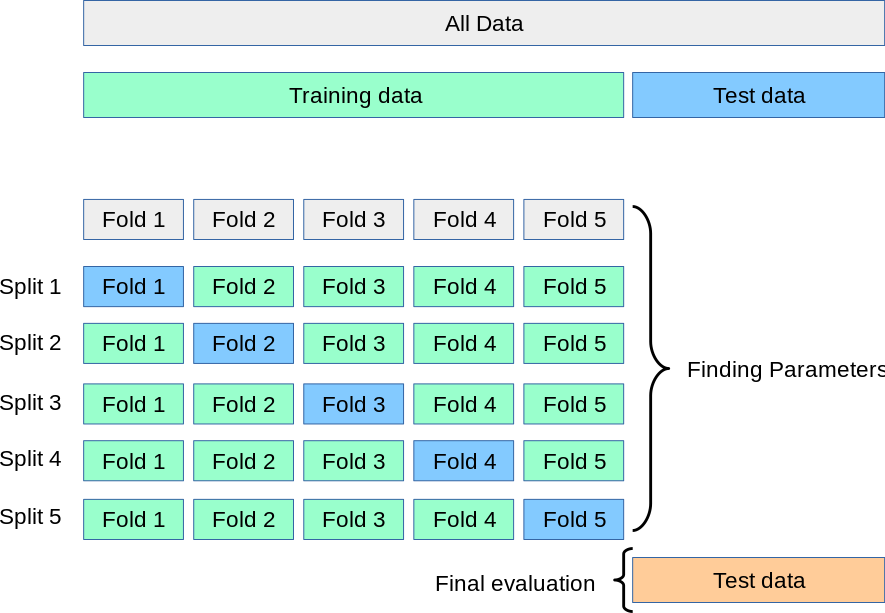
Cross validation